Seven Millennium Problems in Mathematics (Part I)

What is the hardest way to earn 1 million dollars?

For Mathematicians, Solve one of the Millennium problems!

The millennium prize problems are seven of the most well-known and important unsolved problems in mathematics. The Clay Mathematics Institute, a private Non-profit foundation, devoted to mathematical research famously challenged the mathematical community in 2000 to solve these seven problems and establish the one million US dollar reward for the solvers of each. One of the seven problems has been solved and the other six are the subject of a great deal of current research.

Here are the seven Millennium prize problems…

1. Riemann hypothesis

Many of us know the concept of prime numbers. The numbers which have only two factors as 1 and themselves are prime numbers. The distribution of such numbers in real line is not following any pattern (not uniform). The German mathematician G.F.B Riemann is noted that the occurrence frequency of prime numbers is very much close to the following function

This function is nowadays called “Riemann zeta function”.

He found that the solutions of the zeta function are all the even negative numbers. But those numbers are considered as trivial solutions. So later, he defined a hypothesis called Riemann hypothesis.

The Riemann hypothesis states that,

All the non-trivial solutions of Riemann zeta function (i.e. ) are lie on only one vertical line in the critical area. That vertical line has all the complex numbers which has a real part 1/2.

Graphically,

Hence the 10¹³ (i.e. 10,000, 000, 000, 000) and few of a large heights, number of solutions has been checked by Gourdan 2004. In 2020, the number of checked solutions is extended to 12, 363, 153, 437, 138 and up to height 3, 000, 175, 332, 800 by Platt and Trudgian and also verified by Gourdan.

A proof that this hypothesis is true for every non-trivial solution has not yet been found.

2. P vs NP problem:

One of the biggest unsolved problem in computer science field is “The P vs NP problem”.

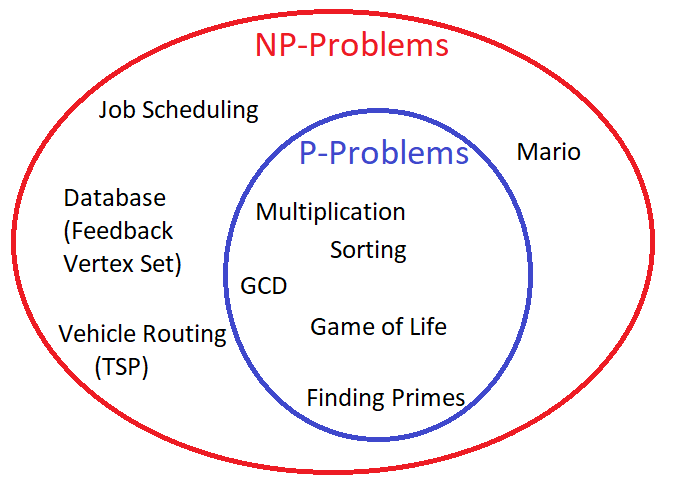
Here, ‘P’ stands for polynomial time and ‘NP’ stands for ‘non-deterministic polynomial time. In general, ‘P’-problems are easier to solve and easier to verify, while ‘NP’-problems are harder to solve but easier to verify.

For example, Multiplication, sorting, finding GCD are the P-problems. Because, it is possible to solve these problems by a certain algorithm in finite number of steps according to the number of inputs and also much easier to verify the final solution.  Most importantly, the time required to solve these type of problems can be defined in terms of polynomial with finite number of terms.

One of the familiar examples for NP-problem is the “SODUKU” game. In this game, the player is given by the partially filled grid and asks to complete the grid with certain conditions. This game is much harder to solve when the grid increases its size. But once the solution was found, it is very easy to check whether it is correct or not. So it is the NP problem. No unique algorithm is defined to solve this game, but it is possible to construct easy algorithm to check the solution. There are many number of solutions may occur. Another example for NP-problem is finding the factors of a number. Suppose if you’re asked to find the different factors of a two digit number say 15, it is easy to find as 3 and 5. But the given number was bigger in size, say 2456345, now it is much harder to find factors. However, once you found the factors, we can easily check whether your answer is correct or not by multiplying together. So we can’t predict the time requires solving these problems, but can predict the time requires to check. In other words, it is not possible to define a finite polynomial time function for an NP-problem.

Some NP-problems can be converted into P-problems by certain shortcuts and some of them or not called NP-Hard. That means, for some cases, P=NP and some other cases P≠NP.

So if you could prove P=NP for all the cases, we may win 1million dollars!

3. Navier-Stokes equation:

The Naiver-Stokes problem deals mostly with the properties of fluids. Fluids are basically things which flow, so they can be liquids, like water, or gases, like oxygen. A whole branch of physics that deals with fluids, is called fluid mechanics.

If we drop a ball on the ground, we can pretty well predict how it’s going to move. According to Newton’s laws, if we know all the features of the ball and its surroundings down to every last detail, then we can predict exactly what the ball is going to do in the future. Fluids aren’t like that. Every time you drop the water, it flows in a different way, and it’s nearly impossible to figure out why this happens.

So why it is that fluid are so different from solids? It’s because of the molecules: In a solid, molecules are close together to the point that they maintain their shape in almost all conditions. Fluid molecules, on the other hand, are variable. They have quite some space to move, and every time there’s even a slight change in the system, they begin to move. Drop a rock into the sea, it has barely any effect, but the water still begins to move.

So what exactly does the Naiver-Stokes equation do?

Well, it takes in certain properties of fluids and gives out the speed of every molecule, using which we can approximately determine the way the fluid will flow.

Firstly, Pressure is one of the characteristic of fluids. If you put water in a glass, it’ll exert a certain amount of pressure on the walls, a pressure powerful enough that it can alter the behavior of the water. This is represented in the Navier-Stokes equation by the pressure gradient, which measures how fast the pressure is changing from instant to instant.

Next, we have a characteristic of fluids: Viscosity. It means ‘thick’ or ‘sticky’. Viscosity is the amount by which a fluid sticks to itself, and tries not to move. Suppose put your finger in a glass of water and try to move it, it’s not very hard. But if you try it again with honey, and you’ll find that it’s much harder to move. Viscosity can radically alter its motion.

Finally, we have the stress tensor: it’s a way of measuring how the fluid is ‘rubbing’ against each other. If you take a book on a table and try to push it parallel to the table, you’ll find that the book bends at an angle. Something similar happens in fluids. They tend to skew against each other. If you imagine a fluid as a collection of very small layers, you’ll find that they keep rubbing and flowing against each other. The stress tensor takes that into account.

The Navier-Stokes equation is

Here, stands for viscosity and represents the acceleration, on the other side of the equation stands for pressure gradient,   is the divergence of the stress and represents  external forces.

This equation works perfectly for all the fluids and air flow problems in 2-dimensional. However, nobody come up with the mathematical proof of the Navier-Stokes equation.

To prove this equation works for all situations with all kind of fluids, one should prove the followings.

1. Solution must exist for all environments
2. That solution must be unique
3. That unique solution must be smooth (i.e. small changes in input results only a small change in output.)

So far, physicists and engineers accepts and using Navier-Stokes equation for many applications. But, for a mathematician, a proper proof is the only way to satisfy them!

We will continue in the next blog….

Acknowledgements….

I am thankful to the following sources for this blog

1. https://www.claymath.org/millennium-problems/millennium-prize-problems
2. https://youtu.be/g5C5bwS4p7s
3. https://youtu.be/eN0DGaMW3Uk
4. https://en.wikipedia.org/wiki/Riemann_hypothesis
5. https://youtu.be/d6c6uIyieoo
6. https://youtu.be/ERBVFcutl3M
7. https://en.wikipedia.org/wiki/Navier-Stokes_equations
8. https://en.wikipedia.org/wiki/P_versus_NP_problem
9. https://youtu.be/YX40hbAHx3s
10. https://youtu.be/EHp4FPyajKQ